Xu Zhang's Homepage

Research Grants

My research has been supported by

NSF Grant DMS-2110833 (PI)
NSF Grant DMS-2005272 (PI)
NSF Grant DMS-1720425 (PI)
ORAU 2021 Powe Junior Faculty Enhancement Award (PI)

Research Interests

Numerical Analysis and Scientific Computing
Numerical Methods for Partial Differential Equations
Finite Element and Discontinuous Galerkin Methods
Immersed Finite Element Methods for Interface Problems
A Posteriori Error Estimation and Adaptive Finite Element Methods
Superconvergence of Finite Element Methods

Research Description

My research focuses on the Immersed Finite Element (IFE) methods for interface problems and their applications. IFE methods can be used to solve both static interface problems and moving interface problems.

Static Interface Problems

In science and engineering, many simulations are carried out over domains consisting of multiple materials which are separated by curves or surfaces. This usually leads to the so-called interface problems of partial differential equations whose coefficients are discontinuous across the material interface. These interface problems can be solved by different types of finite element methods.

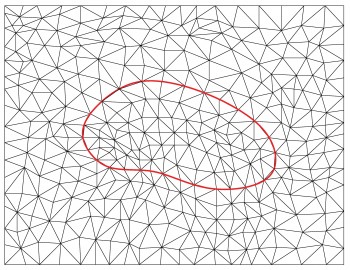
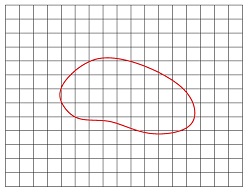
Conventional Finite Element Method can be used to solve the interface problems provided that the solution mesh is tailored to fit the interface geometry (body-fitting mesh). Geometrically, such mesh requires each element to be placed essentially on one side of the interface.

Immersed Finite Element (IFE) Method can use non-body-fitting meshes, such as Cartesian meshes to solve interface problem. IFE basis functions are interface-dependent and they are constructed to fit physical interface jump conditions. We focus on IFE methods for the second order elliptic interface problems and elasticity interface problems. Our research includes both developing efficient IFE methods and carrying out related error estimation.

Related publications:

Cuiyu He, Xu Zhang
Residual based a posteriori error estimation for immersed finite element methods.
Journal of Scientific Computing, 81 (2019), no. 3, 2051-2079.
Tao Lin, Dongwoo Sheen, Xu Zhang
A nonconforming immersed finite element method for elliptic interface problems.
Journal of Scientific Computing, 79 (2019), no. 1, 442-463.
Waixiang Cao, Xu Zhang, Zhimin Zhang
Superconvergence of immersed finite element methods for interface problems.
Advances in Computational Mathematics 43 (2017), no. 4, 795--821.
Tao Lin, Yanping Lin, Xu Zhang
Partially penalized immersed finite element methods for elliptic interface problems.
SIAM Journal on Numerical Analysis 53 (2015), no. 2, 1121-1144.
(Highly cited paper in Mathematics in Web of Science)
Tao Lin, Qing Yang, Xu Zhang
A priori error estimates for some discontinuous Galerkin immersed finite element methods.
Journal of Scientific Computing 65 (2015), no. 3, 875-894.
Tao Lin, Dongwoo Sheen, Xu Zhang
A locking-free immersed finite element method for planar elasticity interface problems.
Journal of Computational Physics 247 (2013), 228-247.

Moving Interface Problems

Many simulations involve moving interfaces such as phase transition problems and free boundary problems. An immediate benefit of using Immersed Finite Element Method is the avoidance of regenerating meshes. More importantly, numbers and locations of degrees of freedom remain unchanged even though interfaces evolve. These features enable us to combine IFEs with the method of lines to efficiently solve moving interface problems on a Cartesian mesh.