This webpage collects data related to veering structures on ideal triangulations of three-manifolds, as introduced by Ian Agol in his 2011 paper, Ideal triangulations of pseudo-Anosov mapping tori. The data and images here were all generated in collaboration with Saul Schleimer, using Regina by Ben Burton, Ryan Budney, William Pettersson, and others. We also provide data derived from our census using SnapPy, written by Marc Culler, Nathan Dunfield, and Matthias Goerner using the SnapPea kernel written by Jeff Weeks.
For the definition of a veering triangulation as used on this webpage, see the paper Veering triangulations admit strict angle structures by Hodgson, Rubinstein, Segerman and Tillmann.
The code we used to generate the census below is part of our repository Veering. The relevant code for the census is here. This script is based on a previous census generating program written by my master's student Andreas Giannopoulos.
The census
Here we restrict to transverse veering structures, meaning that the two-skeleton of the triangulation admits a transverse coorientation compatible with the taut angle structure. However, we do not restrict to layered triangulations.
We build all transverse veering triangulations with up to 16 tetrahedra, for a total of 87,047 veering structures. The census is given in the form of a text file. Each line of the text file is the taut isoSig for a veering triangulation. A taut isoSig is formatted as follows:
[isoSig]_[taut angle structure]
Here, [isoSig] is Regina's isomorphism signature for the triangulation, and [taut angle structure] is a string of numbers that records which pair of edges in each tetrahedron has angle pi. A "0" means that the edges between vertices 0 and 1, and between vertices 2 and 3 in Regina's numbering of that tetrahedron has angle pi. A "1" means the same for the edges between vertices 0 and 2, and between vertices 1 and 3. A "2" means the same for the edges between vertices 0 and 3, and between vertices 1 and 2.
If a triangulation has non-trivial symmetries then it is possible that different taut angle structures on the same triangulation can give the same veering structure. In such a case, we choose the lexicographically earliest taut angle structure string for the taut isoSig.
Note that Regina's method to generate a triangulation from an isoSig does not return an oriented triangulation, even when the triangulation is orientable. To remedy this, we provide a Regina-Python utility script that returns an oriented triangulation, together with the taut angle structure for that oriented triangulation. (In fact, our oriented triangulation is constructed in such a way that its taut angle structure has pis at the same edges of each tetrahedron as that of Regina's triangulation, and hence matches the taut isoSig.) Note that there is no canonical choice of the two possible orientations: we choose one arbitrarily. Reversing the orientation swaps the edge colours.
- Veering - GitHub repository of scripts for working with transverse taut and veering triangulations. The function isoSig_to_tri_angle within taut.py converts a taut isoSig into an oriented triangulation and a corresponding taut angle structure.
- veering_census.txt - The census of transverse veering triangulations, ordered lexicographically by taut isoSig.
- veering_other_names.txt - Veering triangulations on manifolds that SnapPy knows other names for.
- veering_duplicates.txt - Each line of this file is a list of veering isoSigs for the same manifold (when we know of a manifold with more than one). Sometimes we have multiple veering structures on the same triangulation and sometimes we have multiple triangulations for the same manifold. This list was compiled from the 16 tetrahedron veering census using SnapPy's isometry signature (with verified = False, so apply appropriate grains of salt).
- veering_knots.txt - Each line of this file is a veering isoSig for a knot in the three-sphere, together with the slope (using the SnapPy framing) that gives the three-sphere. We find a total of 609 triangulations of knot complements that also admit a veering structure.
- veering_non_geometric.txt - Each line of this file is a veering isoSig for a non-geometric triangulation, checked with snappy's verify_hyperbolicity. The complement of this list is rigourously geometric; triangulations on the list itself are almost certainly not geometric.
- veering_census_with_data.txt - this is a copy of the entire census with extra information: we append to each line the following pieces of data.
- Either 'Fk' or 'Nk' where k is a non-negative integer. The former means that the horizontal branched surface carries a finite depth foliation, and the minimal such has depth k. The latter means that the horizontal branched surface does not carry a finite depth foliation, and we require k cuts to realise that fact. Thus 'F0' means that the veering triangulation is layered and 'N0' means that the horizontal branched surface carries no surface of finite topological type.
- The number of cusps of the manifold.
- Either 'G' or 'N', standing for 'geometric' or 'not geometric', checked with snappy's verify_hyperbolicity.
- The size of the transverse veering symmetry group.
- Either 'E' or 'N', standing for 'edge-orientable' or 'not edge-orientable'.
- The order of the absolute Euler class e in H²(|T|; Z). Here |T| is the realisation of the taut ideal triangulation T. Thus, if this number is 1, the Euler class is zero.
- The number of ladders in each cusp.
- A list of three integers, counting the numbers of toggle tetrahedra, red fan tetrahedra, and blue fan tetrahedra.
- The homology of the manifold.
- A list of other names that SnapPy knows for the manifold.
Here, for each number of tetrahedra we tabulate the number of veering structures, and the number of those structures with various other properties. The data on non-geometric triangulations was generated by SnapPy (and therefore requires further grains of salt).
| tetrahedra | veering structures | zero Euler class | F0 | F1 | F2 | N0 | N1 | non-geometric |
|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 |
| 3 | 3 | 3 | 3 | 0 | 0 | 0 | 0 | 0 |
| 4 | 12 | 12 | 12 | 0 | 0 | 0 | 0 | 0 |
| 5 | 20 | 20 | 16 | 0 | 0 | 4 | 0 | 0 |
| 6 | 50 | 48 | 37 | 1 | 0 | 12 | 0 | 0 |
| 7 | 85 | 83 | 61 | 0 | 0 | 24 | 0 | 0 |
| 8 | 202 | 191 | 142 | 11 | 0 | 49 | 0 | 0 |
| 9 | 355 | 337 | 235 | 29 | 0 | 91 | 0 | 1 |
| 10 | 745 | 690 | 492 | 64 | 0 | 189 | 0 | 3 |
| 11 | 1358 | 1259 | 866 | 99 | 0 | 389 | 4 | 9 |
| 12 | 2867 | 2656 | 1833 | 214 | 1 | 815 | 4 | 22 |
| 13 | 5330 | 4887 | 3255 | 449 | 1 | 1619 | 6 | 52 |
| 14 | 10972 | 10047 | 6709 | 966 | 3 | 3281 | 13 | 110 |
| 15 | 21283 | 19417 | 12497 | 1944 | 11 | 6813 | 18 | 232 |
| 16 | 43763 | 39970 | 25606 | 4017 | 31 | 14039 | 70 | 502 |
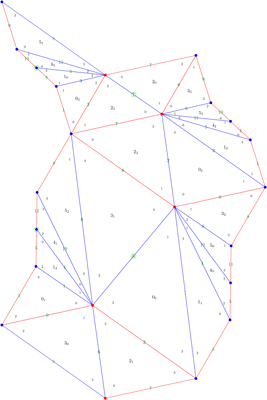
Triangulation of the boundary torus (in the geometric and ladders styles) for the veering
triangulation gLLAQbecdfffhhnkqnc_120012. This manifold is s227 in the SnapPy census.
Induced triangulations of the boundary tori
For veering triangulations from our census up to 12 tetrahedra (5699 veering triangulations), we draw pictures of the induced triangulation of each boundary torus. We now explain these pictures further. We put our eye at a cusp. A tetrahedron incident to that cusp then has at least one of its vertices at our eye. We draw a dot for each edge leaving such a vertex, and we draw the remaining three edges connecting those dots. So each vertex of each tetrahedron gives a triangle on these images. The numbers on the pictures agree with Regina's numbering scheme, as follows. Each triangle is labelled with a tetrahedron number, together with a subscript indicating which of the four vertices of the tetrahedron is at our eye. The three corners of the triangle are labelled with the other three vertices of that tetrahedron. Faces of the triangulation are labelled with green numbers on the corresponding edges of the boundary triangulation. We also draw a green circle at a vertex or edge-midpoint if the triangulation of the boundary torus has a rotational symmetry there. When a manifold has multiple boundary components, we draw them in a column, ordered by Regina's numbering, with the zeroth cusp at the bottom.
We draw these pictures in two styles: geometric - following the geometry induced by the complete hyperbolic structure on the manifold, and ladders - essentially in the style of the pictures in Explicit angle structures for veering triangulations by David Futer and François Guéritaud. We differ from that paper in that we smooth the edges so that they are vertical at each vertex. This makes our ladderpoles straight.
- Veering boundary triangulations (geometric style) up to 6 tetrahedra (directory).
- Veering boundary triangulations (ladders style) up to 6 tetrahedra (directory).
- Veering boundary triangulations (geometric style) up to 12 tetrahedra (zip file).
- Veering boundary triangulations (ladders style) up to 12 tetrahedra (zip file).
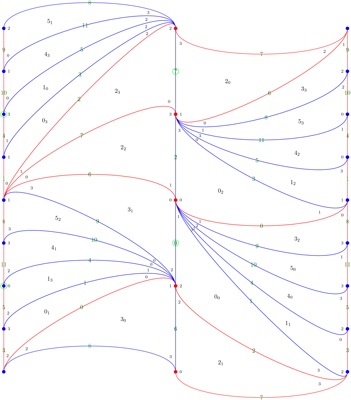
Mid-annuli for gLLAQbecdfffhhnkqnc_120012,
a veering triangulation for the manifold
s227 in the SnapPy census.
Mid-annuli
Following Theorem 5.10 of our paper From veering triangulations to pseudo-Anosov flows, a manifold with a veering triangulation canonically decomposes into a union of veering solid tori. Each veering solid torus has a vertical mid-annulus cutting it in half. The mid-annuli glue together to give the mid-surface. For veering triangulations from our census up to 12 tetrahedra, we draw pictures of the mid-annuli, cut into half-diamonds, which are labelled by the tetrahedra they are in. Each half-diamond sits in either the top or bottom half of a tetrahedron, and has vertices at the midpoints of the majority colour edge in that half-tetrahedron. See Section 5.37 of our paper for further details on the labelling of these mid-surface pictures.
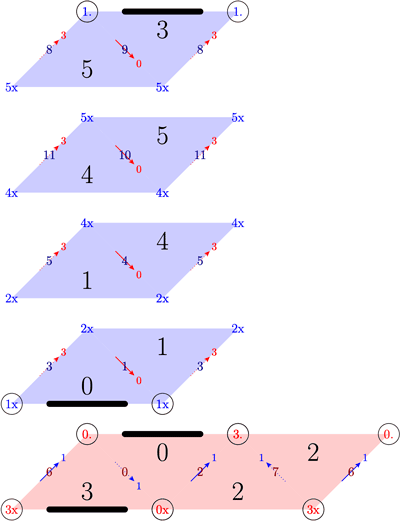
In a separate file, we draw the top two and bottom two triangles of each tetrahedron in a column, with edge and face numbers marked. The same numbers appear on the mid-annuli. We draw edge orientations on the edges in the tetrahedra pictures. These orientations also appear at the corners of each half-diamond on the mid-annuli picture, indicated by either a "." or a "x" after the edge number. These correspond to the arrow pointing out of, or into the screen respectively. Edge numbers have a circle around them when the gluing of the mid-annuli at this edge reverses the orientation on the screen. In particular, we have circles if and only if the mid-surface is non-orientable. Note that our edge orientations are not the same as the orientations given by Regina: we choose our orientations so that as much as possible, two edges of the same colour on the boundary of a triangle have the same orientation relative to their shared vertex.
- Veering mid-annuli up to 6 tetrahedra (directory).
- Veering tetrahedra up to 6 tetrahedra (directory).
- Veering mid-annuli up to 12 tetrahedra (zip file).
- Veering tetrahedra up to 12 tetrahedra (zip file).
Tetrahedra for gLLAQbecdfffhhnkqnc_120012, a
veering triangulation for the manifold s227 in the SnapPy census.
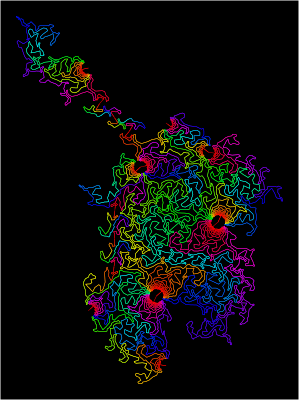

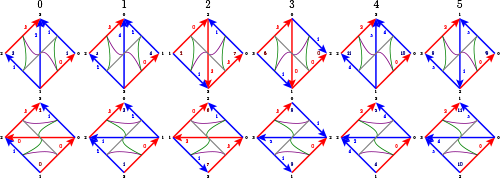
Cannon-Thurston maps (in the spectrum and Jordan styles) for the veering
triangulation gLLAQbecdfffhhnkqnc_120012. This manifold is s227 in the SnapPy census.
Cannon-Thurston Maps
In an upcoming paper with Jason Manning, we show that every veering triangulation induces a Cannon-Thurston map. Here, this is a map from the veering circle into the boundary of three-dimensional hyperbolic space, which is a sphere. This map is space-filling, meaning that the image of the circle hits every point on the sphere. Viewed from a cusp, the Cannon-Thurston map is the same in every fundamental domain of the boundary torus. We draw an approximation to the Cannon-Thurston map in a fundamental domain. These match up with the induced geometric triangulations of the boundary tori given above.
We draw our approximations of Cannon-Thurston maps in two styles: In the spectrum style, we colour the curve by going around the colour wheel as it moves from one vertex of a ladder pole to the next. In the Jordan style, we use the fact that the curve is a Jordan curve, separating the sphere into two parts; we colour these black and white. These pictures depend on a parameter for how closely our curve approximates the true Cannon-Thurston map. Here is a Jordan style picture using the same veering triangulation as in the figure to the right, but with four times better resolution.
- Cannon-Thurston maps in spectrum style with up to 6 tetrahedra (directory).
- Cannon-Thurston maps in Jordan style with up to 6 tetrahedra (directory).
- Cannon-Thurston maps in spectrum style with up to 12 tetrahedra (zip file).
- Cannon-Thurston maps in Jordan style with up to 12 tetrahedra (zip file).
Citation
If you find this census useful in your research, please consider citing it. A suggested reference is:
Andreas Giannopoulos, Saul Schleimer and Henry Segerman. A census of veering structures. https://math.okstate.edu/people/segerman/veering.html, 2019.
Bibtex entry:
@Misc{VeeringCensus,
author = {Giannopoulos, Andreas and Schleimer, Saul and Segerman, Henry},
title = {A census of veering structures},
howpublished = {\url{https://math.okstate.edu/people/segerman/veering.html} {YYYY/MM/DD}}
}
The various visualizations on this page are by Saul Schleimer and Henry Segerman.
This page last updated:



