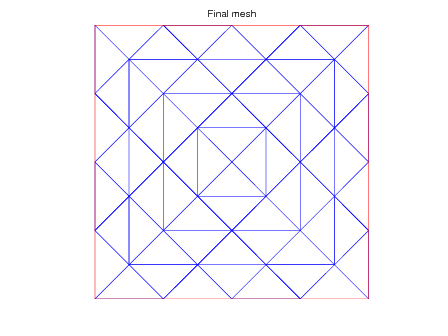
function meshdemo
  % Define a simple mesh on a square domain.
  p = [0,0; 1,0; 0,1; 1,1; 0.5,0.5];
  t = [1,2,5; 2,4,5; 4,3,5; 3,1,5];
  be = [1,2; 2,4; 4,3; 3,1];

  % Draw this simple mesh.
  plotmesh(1,p,be,t,'Initial mesh');

  % Refine the mesh twice and draw the new mesh.
  for i=1:2
    [p,be,t] = refine(p,be,t);
  end
  plotmesh(2,p,be,t,'Final mesh');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Draw the mesh
% Inputs:
%         n_fig  -- id of drawing window
%         p,be,t -- mesh data
%         titletext -- title of this plot
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function plotmesh(n_fig, p,be,t,titletext)
  figure(n_fig); clf; hold on;

  % draw all edges in blue
  for i=1:size(t,1);
    plot(p(t(i,:),1),p(t(i,:),2),'b');
  end

  % draw boundary edge in red
  for i = 1:size(be,1);
    ind = be(i,:);
    plot(p(ind,1),p(ind,2),'r');
  end

  hold off,axis equal,axis off
  title(titletext);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Refine the mesh uniformly
% Inputs:
%         p,be,t -- original mesh
% Outputs:
%         P,BE,T -- refined mesh
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [P, BE, T] = refine(p,be,t)
  % number of points, triangles, boundary edges, and edges
  np = size(p,1);
  nt = size(t,1);
  nbe = size(be,1);
  ne = (3*nt + nbe)/2;

  % Since we only have information about boundary edges,
  % here we need to reconstruct edges (including internal ones).
  % Notice that edges can be understood as the adjacency relation
  % of vertices, we first build the vertex adjacency table.
  % Here we also use the concept of "half edge".
  % A "half edge" is an edge in a triangle associated with the
  % positive (counter-clockwise) direction in this triangle.
  % Each internal edge can be viewed as two "half edges" pointing at
  % opposite directions, from the two triangles sharing this edge.
  % Each boundary edge has only one "half edge".
  %
  % p2p_adjacency_table:
  %    If the (i,j)th entry of this table is 1,
  %    then there is a "half edge" from the ith to the jth vertices.
  %    If both (i,j) and (j,i) are 1, then this is an internal edge.
  %    Otherwise, it is a boundary edge.
  %
  % e2t_table:
  %    When the (i,j)th entry of p2p_adjacency_table is 1,
  %    the (i,j)th entry of e2t_table stores the index
  %    of the triangle where this "half edge" is defined.
  %
  p2p_adjacency_table = sparse (np, np);
  e2t_table =sparse(np, np);
  for i = 1:nt
    for j = 1:3
      row = t(i,j);
      col = t(i,mod(j,3)+1);
      p2p_adjacency_table (row, col) = 1;
      e2t_table (row, col) = i;
    end
  end

  % Once we have p2p_adjacency_table and e2t_table,
  % we can build the edge table e, which is a ne-by-5 matrix.
  % Each row corresponds to one edge (internal and boundary).
  % For internal edges, we need to combine the two "half edges"
  % into one edge. For each edge, we need to specify
  % its starting and ending vertices. This is done by simply
  % chosing the starting vertex to be the vertex with a
  % smaller index. Notice this may give a direction different from
  % direction specified in the matrix be (boundary edges).
  %
  % Each row of matrix e contains 5 elements
  % in the following order:
  %      starting_vertex_index : always the smaller index
  %      ending_vertex_index   : always the larger index
  %      is_boundary_edge      : =1 if this edge is on boundary
  %      left_triangle_index   : index of the left triangle
  %      right_triangle_index  : index of the right triangle
  %
  % For boundary edges, either left_triangle_index or
  % right_triangle_index is 0.
  e = zeros(ne,5);
  edgeindex = 1;
  for i = 1:np
    for j=(i+1):np
      adjacency = p2p_adjacency_table (i,j) + p2p_adjacency_table (j,i);
      if ( adjacency ~= 0 )
	e(edgeindex, 1:2) = [i,j];
	% Mark boundary edges
	if ( adjacency == 1 )
	  e(edgeindex, 3) = 1;
	end
	e(edgeindex, 4) = e2t_table (i,j);
	e(edgeindex, 5) = e2t_table (j,i);
	edgeindex = edgeindex + 1;
      end
    end
  end

  % Generate triangle-to-edge table t2e_table.
  % Each row of this table stores the index of three edges
  % in a triangle.
  t2e_table = zeros(nt,3);
  for i=1:ne
    if (e(i,4)>0)
      t2e_table ( e(i,4), find(t(e(i,4),:)==e(i,1)) ) = i;
    end
    if (e(i,5)>0)
      t2e_table ( e(i,5), find(t(e(i,5),:)==e(i,2)) ) = i;
    end
  end

  % Now we are ready to build the refined mesh P,BE,T.
  nP = np + ne;
  nT = 4*nt;
  nBE = 2*nbe;
  P = zeros(nP,2);
  T = zeros(nT,3);
  BE = zeros(nBE,2);

  % Generate P
  % P contains all original points in p
  % and center points of each edge in e
  P(1:np,:) = p;
  for i=1:ne
    P(np+i,:) = sum (p(e(i,1:2),:))*0.5;
  end

  % Generate BE
  % BE inherits the orientation of be.
  for i=1:nbe
    j = 1;
    while max( e(j,1:3) ~= [min(be(i,:)), max(be(i,:)), 1] )
      j = j+1;
    end
    BE([2*i-1, 2*i], :) = [be(i,1), np+j; np+j, be(i,2)];
  end

  % Generate T
  % Each triangle in t is divided into 4 small triangles
  for i=1:nt
    temp = [t(i,:), np+t2e_table(i,:)];
    T((4*i-3):(4*i), :) = [ temp(1), temp(4), temp(6);
                            temp(2), temp(5), temp(4);
			    temp(3), temp(6), temp(5);
			    temp(4), temp(5), temp(6)];
  end

Published with MATLAB® 7.6