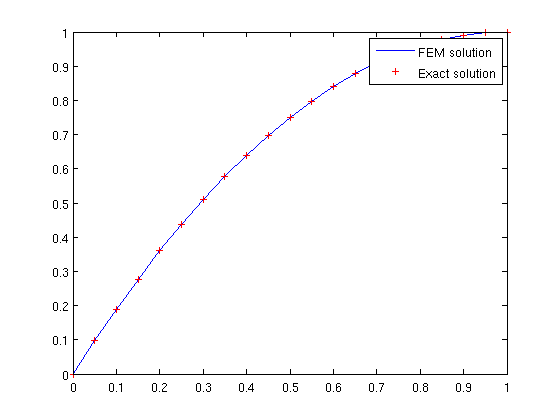
function fem1dlinear % This function solves the 1D BVP % -au'' + bu' + cu = f in (x0, x1) % with either Dirichlet or Neumann boundary conditions at x0 and x1. % % The problem is solved using a finite element method % using the continuous piecewise linear approximation space. % % % Variables % ========================================= % coefficients: a structure containing three coefficients a,b,c in the equation. % They are stored in coefficients.a, coefficients.b, coefficients.c % % leftbdr, rightbdr: Two structures defining the boundary conditions on x0 and x1. % Each contains three components, we use leftbdr as an example: % leftbdr.x = x0 % leftbdr.type is either 'Dirichlet' or 'Neumann' % leftbdr.value: for Dirichlet boundary condition, it is % the value of u(x0); for Neumann boundary % condition, it is the value of u'(x0) % The definition of rightbdr is similar. % % f: the right-hand function. It is defined using "function handle". % See matlab help for more about function handle. % % n: number of sub-intervals. % % x: A row vector containing the x-coordinates of all grid nodes. % It needs to be monotonically increasing, and x(1) = x0, x(end) = x1. % % A, rhs, u: the linear system derived from the finite element approximation is % A u = rhs % % % Subroutines % ========================================= % assembleLocalMatrix % assembleLocalRhs % % ===================================================================== % PART I: initialization % ===================================================================== % In this part, we set up the problem. % You can change the settings here in order to solve a different problem. % setting coefficients coefficients.a = 1; coefficients.b = 5; coefficients.c = 5; % set left boundary condition leftbdr.x = 0; leftbdr.type = 'Dirichlet'; leftbdr.value = 0; % set right boundary condition rightbdr.x = 1; rightbdr.type = 'Neumann'; rightbdr.value = 0; % set right-hand side function f f = @(x) 12-5*x.*x; % set number of intervals and generate grid % For now, a uniform grid is generated. % One can rewrite this part to generate a non-uniform grid. n = 20; x = linspace(leftbdr.x, rightbdr.x, n+1); % ===================================================================== % PART II: finite element discretization % ===================================================================== % In this part, we assemble the linear system using the finite element method. % Then solve the linear system. % assemble matrix A A = sparse(n+1,n+1); for i=1:n % on each sub-interval [x(i), x(i+1)] localmat = assembleLocalMatrix(x(i),x(i+1),coefficients); A(i:i+1,i:i+1) = A(i:i+1,i:i+1) + localmat; end % assemble right-hand side vector rhs = (f,v) rhs = zeros(n+1,1); for i=1:n % on each sub-interval [x(i), x(i+1)] localrhs = assembleLocalRhs(x(i),x(i+1),f); rhs(i:i+1) = rhs(i:i+1) + localrhs; end % apply left boundary condition if strcmp(leftbdr.type, 'Dirichlet') % make the first row (1,0,0,...,0), and set rhs(1) A(1,:) = 0; A(1,1) = 1.0; rhs(1) = leftbdr.value; % change 2:end entries of rhs, % then erase 2:end entries in the first column of A rhs(2:end) = rhs(2:end) - A(2:end,1) * leftbdr.value; A(2:end,1) = 0; else % Neumann bdr condition rhs(1) = rhs(1) - coefficients.a * leftbdr.value; end % apply right boundary condition if strcmp(rightbdr.type, 'Dirichlet') % make the last row (0,...,0,0,1), and set rhs(end) A(end,:) = 0; A(end,end) = 1.0; rhs(end) = rightbdr.value; % change 1:end-1 entries of rhs, % then erase 1:end-1 entries in the last column of A rhs(1:end-1) = rhs(1:end-1) - A(1:end-1,end) * rightbdr.value; A(1:end-1,end) = 0; else % Neumann bdr condition rhs(end) = rhs(end) + coefficients.a * rightbdr.value; end % solve u = A \ rhs; % ===================================================================== % PART III: print out the result % ===================================================================== % for the current problem, we know that its exact solution is % u = x(1-x) plot(x, u, 'b', x, x.*(2-x), 'r+'); legend('FEM solution', 'Exact solution'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % This is the end of the main function. % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % ===================================================================== % PART IV: subroutines % ===================================================================== % This part contains some sub-functions. %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % This is to compute (au',v') + (bu',v) + (cu,v) % on the subinterval [a,b] function localA = assembleLocalMatrix(a,b,coefficients) h = b-a; localA = coefficients.a / h * [1, -1; -1, 1] ... + coefficients.b * [-0.5, 0.5; -0.5, 0.5] ... + coefficients.c * h * [1/3, 1/6; 1/6, 1/3]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % This is to compute (f,v) on the subinterval [a,b]. % A Gaussian quadrature will be used to evaluate the % integral. Here we use a 5th order scheme. You can % change "5" into what ever order you would like to use. function localrhs = assembleLocalRhs(a,b,f) % First, compute the Gaussian points and weights. % Both gaussianpoints and gaussianweights are column vectors. [gaussianpoints, gaussianweights] = lgwt(5,a,b); % evaluate the value f on Gaussian points % fvalue is a column vector fvalue = f(gaussianpoints); % evaluate the value of two basis functions % (b-x)/(b-a) and (x-a)/(b-a) % on gaussianpoints. % "shape" is a matrix with two columns, each column % contains the value of one basis function on gaussianpoints. h = b-a; shape = [ (b-gaussianpoints)/h, (gaussianpoints-a)/h ]; % apply the gaussian quadrature to compute localrhs localrhs = shape' * (fvalue.*gaussianweights);