Segre-degenerate points form a semianalytic set

Segre varieties, vaguely: the set gotten by keeping $\bar{z}$ fixed, are a useful tool in CR geometry.

For example, they locate complex manifolds inside real manifolds (and subvarieties).

For a Levi-flat hypersurface, they give exactly the Levi-foliation.

They have seen much use on real-analytic manifolds since being first used in CR geometry by Webster and also Diederich–Fornæss in the 1970s. There are way too many papers to cite here.

Recently, they started to be used on singular subvarieties, e.g., Burns–Gong '99, Diederich–Mazzilli '08, Fernández-Pérez '14, Adamus–Randriambololona–Shafikov '17, Pinchuk–Shafikov–Sukhov '17, Yours Truly, etc.

But, however tempting it may be, not all of the techniques carry over to the singular setting.

"Begin at the beginning," the King said, very gravely, "and go on till you come to the end: then stop."

                                                                —Lewis Carroll

Let $U \subset {\mathbb{R}}^k$ be open. $X \subset U$ is a real-analytic subvariety if at each point $p \in U,$ there is a neighborhood $V$ and a family of real-analytic functions ${\mathcal{F}}(V)$ such that

\[ X \cap V = \{ p \in V : f(p) = 0 \text{ for all } f \in {\mathcal{F}}(V) \} . \]

If $U \subset {\mathbb{C}}^k$ and ${\mathcal{F}}(V)$ are holomorphic, then $X$ is a complex-analytic subvariety.

The set of regular points is defined by

\[ X_{\text{reg}} \overset{\text{def}}{=} \{ p \in X : \exists \text{ nbhd. $V$ of $p$ s.t. } V \cap X \text{ is a $C^\omega$ submfld.} \} . \]

(complex submanifold if complex subvariety)

The set of singular points is the set $X_{\text{sing}} = X \setminus X_{\text{reg}}.$

For $p \in X_{\text{reg}},$ write $\dim_p X$ for the dimension of the manifold at $p.$

(complex dimension if $X$ is complex)

\[ \dim_p X \overset{\text{def}}{=} \limsup_{q \in X_{\text{reg}} \to p} \dim_q X \]

\[ \dim X \overset{\text{def}}{=} \max_{p \in X} \dim_p X \]

$X$ is irreducible if $X = A \cup B$ for subvarieties $A$ and $B$ means $A=X$ or $B=X.$

$I_p(X)$ be the ideal of germs of real-analytic functions (resp. holomorphic) vanishing on $X$ at $p.$

Just because we have generators of $I_p(X)$ does not mean those generators will give $I_q(X)$ for $q$ near $p.$

If we can find a single set of generators whose germs generate $I_q(X)$ at all points $q$, then $X$ is coherent (the sheaf of germs of real-analytic functions vanishing on $X$ is a coherent sheaf).

Complex subvarieties are coherent. Real subvarieties need not be.

Example: (Whitney umbrella) Let $X$ be given by $(x,y,s) \in {\mathbb{R}}^3$ by $sx^2=y^2.$ It looks like:

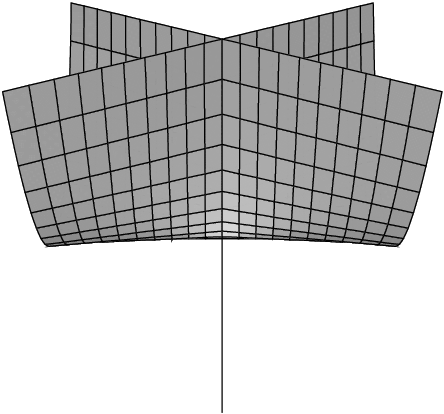
• $X$ is irreducible.

• $\dim_p X$ is not constant.

• $X$ is not coherent. $I_{(0,0,0)}(X)$ has a single generator, but the "handle" requires the generators $x$ and $y.$

Example: Let $X$ be given by $(x,y,s) \in {\mathbb{R}}^3$ by $(x^2+y^2)^6 -s^8x^3(s-x)=0.$ It looks like:

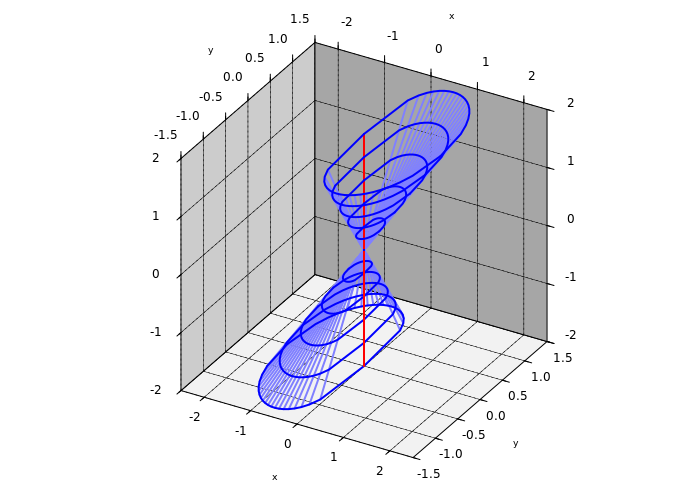
• $X$ is irreducible.

• $X_{\text{sing}}$ is isolated.

• $\dim_p X = 2$ for all $p \in X.$

• For any real-analytic $\psi$ defined near the origin such that $\psi=0$ on $X,$ we have $d\psi(0,0,s) = 0$ for all $s$ (the red line).

• $X$ is not coherent, no function in $I_{(0,0,0)}(X)$ can generate $I_{(0,0,s)}(X)$ for $s \not=0.$

In particular, $d\psi =0$ does not define the singular set. Not even a set of the right dimension.

For a real subvariety $X$, the singular set $X_{\text{sing}}$ need not be a subvariety.

E.g. the Whitney umbrella.

Let $\sS\bigl(C^\omega(V)\bigr)$ be the smallest family of sets that is closed under finite unions, finite intersections, and complements of sets of the form

\[ \bigl\{ x \in V : f(x) \geq 0 \bigr\} \]

where $f \in C^\omega(V).$

$X \subset U$ is semianalytic (in $U$) if for each $p \in U,$ there is a neighborhood $V$ of $p$ such that $X \cap V \in \sS\bigl(C^\omega(V)\bigr).$

If $X$ is a real subvariety, then $X_{\text{sing}}$ is semianalytic.

Let $U \subset {\mathbb{C}}^n={\mathbb{R}}^{2n}$ be open and $X \subset U$ a real-analytic subvariety.

Write $U^{\text{conj}} = \{ z : \bar{z} \in U \}.$

Define $\iota \colon \C^n \to \C^n \times \C^n$ by $\iota(z) = (z,\bar{z}).$ The set

\[ \iota(\C^n) \subset \C^n \times \C^n \]

is called the diagonal.

Let $\sX^U$ be the smallest complex-analytic subvariety of $U \times U^{\text{conj}}$ such that $\iota(X) \subset \sX^U.$

Let $\sX_p$ denote the smallest germ of a complex analytic subvariety $\bigl(\C^n \times \C^n, (p,\bar{p}) \bigr)$ such that \[ \iota\bigl((X,p)\bigr) \subset \sX_p \]

$\sX_p$ is the complexification of the germ $(X,p).$

We can't always find a single complex variety in $\C^n \times \C^n$ whose germs are the complexifications $\sX_p.$

Unless $X$ is coherent.

Let $X \subset U \subset \C^n$ be a subvariety, $p \in X.$

Definition: Say $U$ is good for $X$ at $p \in X$ if the following conditions are satisfied:

(i) $U$ is connected.

(ii) $\dim (X,p) = \dim X = \dim \sX_p = \dim \sX^U$

(iii) $\exists$ real-analytic $\psi \colon U \to \R^k,$ whose complexification converges in $U \times U^{\text{conj}},$ whose zero set is $X,$ and the germ $(\psi,p)$ generates $I_p(X).$

(iv) $\sX^U \cap \iota(\C^n) = \iota(X).$

(v) $\bigl( \sX^U , (p,\bar{p}) \bigr) = \sX_p.$

(vi) Irreducible components of $\sX^U$ correspond to irreducible components of $\sX_p.$

Proposition: For any $p \in X$ a good neighborhood exists (and in fact an arbitrarily small good neighborhood exists).

Suppose $X \subset U \subset \C^n$ and $p \in X.$

Definition: The Segre variety of $X$ at $p\in U$ relative to $U$ is

\[ \Sigma_p^U X \overset{\text{def}}{=} \bigl\{ z \in U : (z,\bar{p}) \in \sX^U \bigr\} . \]

If $U'$ is good for $X$ at $p \in X,$ define the germ

\[ \Sigma_p X \overset{\text{def}}{=} \bigl(\Sigma_p^{U'} X, p \bigr) . \]

Define

\[ X_{[k]} \overset{\text{def}}{=} \bigl\{ z \in U : \dim \Sigma_z X \geq k \bigr\} , \]

\[ X_{U [k]} \overset{\text{def}}{=} \bigl\{ z \in U : \dim_z \Sigma_z^U X \geq k \bigr\} . \]

For a moment, let $X \subset \C^n$ be a real hypersurface.

Normally $\dim \Sigma_p X = n-1.$ We say that $X$ is Segre-degenerate at $p$ if $\Sigma_p X = (\C^n,p).$

So $X_{[n]}$ is the set of Segre-degenerate points for a hypersurface.

Proposition: Suppose $X \subset U \subset \C^n,$ $p \in X,$ and $U$ is good for $X$ at $p.$

Then $X_{U[k]}$ is a real-analytic subvariety.

If $X$ is a hypersurface, $X_{U[n]}$ is a complex analytic subvariety of $X$ of (complex) dimension at most $n-2.$

Sketch of proof: (for a hypersurface)

By reality, if $r$ is a defining function, then $r(p,\bar{q}) = 0$ if and only if $r(q,\bar{p}) = 0.$

So $q \in \Sigma_p^U X$ if and only if $p \in \Sigma_q^U X.$

Intersect all the $\Sigma_q^U X$ for all $q \in U.$

"QED!"

However, there be dragons:

$\Sigma_q^U X$ need not be equal to $\Sigma_q X$ if $q \not=p.$

We do have

\[ \Sigma_q X \subset (\Sigma_q^U,q) . \]

But this is possibly not equality. No matter how small a neighborhood $U$ of $p$ we pick.

Theorem: Let $U \subset \C^n$ be open and $X \subset U$ a real-analytic subvariety of codimension 1. Then:

(i) $X_{[n]}$ is a closed semianalytic set of dimension at most $2n-4,$ which is locally contained in a complex-analytic subvariety of (complex) dimension at most $n-2.$

(ii) If $X$ is coherent, then $X_{[n]}$ is a complex-analytic subvariety of (complex) dimension at most $n-2.$

Theorem: Let $U \subset \C^n$ be open and $X \subset U$ a real-analytic subvariety of dimension $d < 2n$ (i.e. $X \not= U$). Then:

(i) For every $k = 0,1,\ldots,n,$ $X_{[k]}$ is a closed semianalytic subset of $X,$ and $X_{[n]}$ is locally contained in a complex-analytic subvariety of dimension at most $n-d-1.$

(ii) If $X$ is coherent, then for every $k=0,1,\ldots,n,$ $X_{[k]}$ is a closed real-analytic subvariety of $X,$ and $X_{[n]}$ is a complex-analytic subvariety of dimension at most $n-d-1.$

Example: The set of Segre-degenerate points of a coherent hypersurface in $\C^n$ can be a complex subvariety of dimension strictly less than $n-2$:

Define $X$ in $(z,w,\xi) \in \C^3$ by

\[ z\bar{z} + w\bar{w} - \xi \bar{\xi} = 0. \]

• $X_{\text{sing}}$ is isolated

• $X_{[2]} = X,$ $X_{[3]} = \{ 0 \}.$

Example: The set $X_{[k]}$ for $k < n$ is generally not complex.

If $k \leq d-n,$ then $X_{[k]} = X.$

Define $X$ in $(z,w,\xi) \in \C^3$ by

\[ z\bar{z} - w\bar{w} = 0, \qquad \Im \xi = 0 . \]

• $\dim X = 4,$ and $X$ is coherent

• $X_{[1]} = X,$ $X_{[2]} = \{ z=0, w=0, \Im \xi = 0 \},$ and $X_{[3]} = \emptyset.$

Example: A submanifold may be Segre-degenerate (if CR singular).

In $(z,w) \in \C^2,$ let $X$ be

\[ w = z\bar{z} . \]

Actually there is another equation $\bar{w} = z\bar{z}$ to get the complexification right.

• If $(z,w) \in X$ and $z \not= 0,$ then $\Sigma_{(z,w)} X = \{ (z,w) \}.$

• $\Sigma_{(0,0)} X = \{ w = 0 \}$ (as germs).

• $X_{[0]} = X,$ $X_{[1]} = \{ (0,0) \},$ and $X_{[2]} = \emptyset.$

Example: Segre variety of a submanifold can be singular: In $(z,w,\xi) \in \C^3$ define $X$ by

\[ w = z^2+\bar{z}^2+\xi^2+\bar{\xi}^2 . \]

• $\Sigma_{0} X$ is the germ $\{ w = 0, (z+i\xi)(z-i\xi) = 0 \}.$

Example: Consider $(x^2+y^2)^6-s^8x^3(s-x) = 0$ extended to $\C^2$ using $z = x+iy$ and $w = s+it.$

That is,

\[ f(z,w,\bar{z},\bar{w}) = (z\bar{z})^6-(\Re w)^8(\Re z)^3(\Re w-\Re z) = 0 . \]

This $f$ generates $I_0(X)$ and $df = 0$ if $z=0,$ but $X$ is regular outside of $\{ z = 0 , \Re w = 0 \}.$

There are regular points (of hypersurface type) of $X$ where the complexified $f$ defines a singular subvariety.

That is, there are regular points of $X$ where $\sX^U$ is singular.

So no matter how small $U$ is, there are points $q \in U$ where $\Sigma_q^U X$ is singular at $q$ and $\Sigma_q X$ is regular.

That is, \[ \Sigma_q X \subsetneq (\Sigma_q^U,q) . \]

Example: The set of Segre-degenerate points of a hypersurface need not be a subvariety for noncoherent $X.$

Define $X$ in $(z,w,\xi) \in \C^3$ by

\[ z\bar{z} - (\xi+\bar{\xi}) w \bar{w} = 0 . \]

Like the Whitney umbrella.

• $X_{U[3]} = \{ w = z = 0 \}$ (same for any good $U$).

• Where $\Re \xi < 0,$ $X$ is just locally $\{w=z=0 \},$ so $\Sigma_p X$ is one dimensional there.

So \[ X_{[3]} = \{ (z,w,\xi) \in X : w=z=0, \Re \xi \geq 0 \} \]

and this is not a subvariety, it is a semianalytic set.

Also \[ X_{[3]} \subsetneq X_{U[3]} . \]

Example: There exists a (noncoherent) hypersurface in $\C^3$ where the set $X_{[n]}$ of Segre-degenerate points is not complex (it is a real line).

Define $X$ in $(z,w,\xi) \in \C^3$ by

\[ \psi = w^2\bar{w}^2 (\Re \xi) + 4(\Re z)(\Re \xi)^2 w \bar{w} + 4(\Re z)^3 z \bar{z} = 0 . \]

• $\psi$ generates the ideal $I_0(X).$

• $\{ d \psi = 0 \} = \{ \Re z = 0, w = 0 \}$ (so 3-dimensional)

• $X_{\text{sing}} = \{ \Re z = w = \Re \xi = 0 \}$ so $\dim X_{\text{sing}} = 2.$

• $X_{[n]} = \{ z=0, w=0, \Re \xi = 0 \},$ so $X_{[n]}$ is real and $\dim X_{[n]} = 1.$

• For any $U$ good for $X$ at $0,$ we have that (near the origin) $X_{U[n]} = \{ z = 0, w=0 \}.$ It is a complex line.

• $X_{U[n]} \cap X_{\text{reg}} \not=\emptyset.$

The point really is that we can "solve" for $w\bar{w}$ as \[ w\bar{w} = x\left(-2s\pm \frac{2}{s}\sqrt{s^4-s x (x^2+y^2)} \right). \]

And now outside the singular set we can solve for $x$ by implicit function theorem.

Thank you for your attention!