Mistakes which Frequently Occur in College Algebra, and in turn, Technical Calculus.
Below is a list of mistakes which frequently occur in College Algebra. Technical Calculus uses algebra extensively, so these mistakes occur frequently in Technical Calculus too. How many have you been guilty of making? This list is provided to give you an opportunity to learn from the mistakes of others.
Mistake
1: ![]()
Example to show that it
is a mistake:
![]()
Notice ![]() .
.
Correct Rule:
![]() , provided
, provided ![]() and
and ![]()
Mistake
2: ![]()
Example to show that it is a mistake:
![]()
Notice ![]() .
.
Correct Rule:
![]()
Mistake
3: ![]()
Example to show that it
is a mistake:
![]()
Notice ![]() .
.
Correct Rule: A factor
can only be canceled if it is a common factor of
each term in the numerator and
the denominator of a fractional expression.
The term c is not a common
factor of each term in the numerator or the
denominator.
Mistake
4: ![]()
Example to show that it is a mistake:
![]()
Notice ![]() .
.
Correct Rule: A factor
can only be canceled if it is a common factor of
each term in the numerator and
the denominator of a fractional expression.
The term d is not a
common factor of each term in the numerator.
Mistake
5: The meaning of and the rules for the negative sign
The negative sign, “![]() “ can be a source for mistakes
creeping into your work. This short review is intended to make you aware of the
ways in which the negative sign can be used in doing mathematics. The first way
the negative ever appeared to you was its use as a symbol to denote
subtraction, as in
“ can be a source for mistakes
creeping into your work. This short review is intended to make you aware of the
ways in which the negative sign can be used in doing mathematics. The first way
the negative ever appeared to you was its use as a symbol to denote
subtraction, as in ![]() . In this setting the negative sign denoted the process of
“taking away” an amount from a larger amount.
. In this setting the negative sign denoted the process of
“taking away” an amount from a larger amount.
As you progressed in your mathematical studies, the
negative sign was, next, introduced to signify “negative numbers,” numbers to
the left of the number 0 on the number line. e.g.,
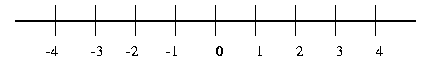
In this context the negative sign was used to denote
an additional collection of numbers, the negative numbers. Addition was defined
on this enlarged set of numbers and the negative numbers were recognized to be
additive inverses of their positive counterpart. Recall what an additive
inverse is.
Additive Inverses: The additive inverse of a
number b is –b. The additive inverse is defined to be the number, when added to
b, which gives the result 0. Examples of additive inverses are:
The
additive inverse of 2 is –2: ![]()
The
additive inverse of –2 is –(-2):![]()
Notice
that ![]()
This
says that ![]() .
.
Notice that the notion of additive inverse and
addition on negative numbers corresponds to our old definition of subtraction
of one number from a larger number. For example, the addition of 17 and the
additive inverse of 9, i.e., ![]() , gives the result 8:
, gives the result 8:
![]()
and this matches with the old
subtraction problem: ![]() The introduction of
negative numbers and the operation of addition on the collection of integers
(positive, zero, and negative) continues to work just as it did when we wished
to subtract a positive number from a larger positive number. In mathematics we
call this process the process of extending addition to the larger set of
integers.
The introduction of
negative numbers and the operation of addition on the collection of integers
(positive, zero, and negative) continues to work just as it did when we wished
to subtract a positive number from a larger positive number. In mathematics we
call this process the process of extending addition to the larger set of
integers.
What happens if we wish to subtract two integers,
regardless of their signs? Do you recall the subtraction rule for![]() where a and b are two integers? This rule, if not remembered, can
be a source of mistakes:
where a and b are two integers? This rule, if not remembered, can
be a source of mistakes:
The Subtraction Rule
![]()
The following examples show this rule in action in a number of
different cases. Examine these cases for patterns to help you avoid mistakes
with the subtraction of two integers.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Another rule to remember when working with negative
numbers is the rule which describes how the negative and positive signs behave
when numbers are multiplied. These rules are given below.
The product of two numbers with like signs is
positive, i.e.,
![]()
The product of two numbers with unlike signs is
negative, i.e.,
![]()
Mistake 6: Don’t be stingy with the use of parentheses
Parentheses are an important
notational device which helps to keep your
mathematical work organized and free of
ambiguity. For example, what is your answer to the simple mathematical expression.
![]() ?
?
Many who compute this expression will work from left
to right as follows:
![]()
![]()
50.
Others will apply the hierarchy (or order) of
operations that they learned in high school algebra to computing the
expression. The hierarchy of operations is sometimes referred to as the “My Dear
Aunt Sally” rule. This rule states that in any mathematical expression
which contains a mixture of arithmetic operations, all multiplications should
be executed first, all divisions should be executed second, all additions
third, and all subtractions last. The order or hierarchy of these four
operations is Multiplication, Division, Addition, and Subtraction,
in other words “My Dear Aunt Sally.” Applying
the order of operations to the expression above yields:
![]()
26;
a different result then we
obtain if we compute from left to right.
Parentheses can be used be
effectively to clear up the inherent ambiguity of the
expression ![]() . For example,
. For example,
![]()
and
![]()
Recall that parentheses are a means
of grouping the order of operations. When
working with expressions involving
parentheses, no matter how complicated the expression is, start your arithmetic
or algebraic computations with those expressions that are found in the
innermost parentheses. Then when the innermost expressions are computed, move
to the next level of parentheses in order to compute the expressions contained
in them. In this fashion, by moving with your computations from the innermost
parentheses to the outermost parentheses you will eventually complete the
computation correctly.
Parentheses are also valuable in keeping track of
the distribution of a product across a sum, especially in algebraic
expressions. Recall the Distributive Property describes how multiplication
distributes across addition:
![]()
For example, as we illustrated earlier, suppose the problem is to solve the
following for x:
![]()
A student’s solution can look like this:
![]()
![]()
![]()
![]()
The correct solution with the appropriate use of parentheses is:
![]()
![]()
![]()
![]()
Notice how the use of
parentheses aids the correct application of the Distributive
Property in the solution
above.
Sometimes expressions can be very complicated,
nested several layers deep with parentheses. A helpful tip to keep in mind when
dealing with parentheses in complicated mathematical expressions is that they
always come in pairs, a left parenthesis must have a right parenthesis to which
it is associated. In the event that you encounter trouble computing a
complicated expression, check to see that it has all of its parentheses by
counting the left ones and the right ones. The count should be identical. If
not, then something is wrong somewhere.
Mistake 7: Dividing by fractional expressions
You know the rule for dividing by fractions. Most
students remember it this way: “invert and multiply.” But the rule is more
precise than the phrase “invert and multiply.” To be precise,
![]()
By and large, the rule in this form does not give
students too much trouble. Students begin to encounter difficulty with “invert
and multiply” when faced with algebraic expressions like:
![]()
What does this fractional expression really mean?
Does it mean
![]() or
or ![]()
These are two different mathematical expressions:
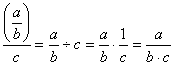
and
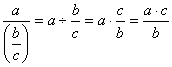
Notice that again we have a case where the prudent
use of parentheses helps to clear up an expression which is definitely
ambiguous.
Mistake 8: Recopying a mathematical
expression incorrectly
Have you ever been guilty of the mistake of
incorrectly copying a previous line of mathematical work? For example, suppose
the problem was to find the solutions of the equation ![]() . This cubic polynomial factors nicely into
. This cubic polynomial factors nicely into
![]()
yielding the solutions of ![]()
![]() ,
, ![]() . If you had the misfortune to copy this problem down as
. If you had the misfortune to copy this problem down as ![]() , then the factors change giving
, then the factors change giving
![]()
and solutions ![]()
![]() , 2. Your answer is wrong, but you are likely to receive some
partial credit for this work on an exam since you have followed through by
factoring the polynomial to find the solutions. If this has ever happened to
you, consider yourself incredibly lucky to get out of messing up a sign so
nicely.
, 2. Your answer is wrong, but you are likely to receive some
partial credit for this work on an exam since you have followed through by
factoring the polynomial to find the solutions. If this has ever happened to
you, consider yourself incredibly lucky to get out of messing up a sign so
nicely.
Consider this, more typical example. Suppose the
problem is to find the solutions of the equation ![]() . Again this cubic polynomial factors nicely into
. Again this cubic polynomial factors nicely into
![]()
giving as solutions ![]() , 1, 2. If, however, on this polynomial any sign is
incorrectly copied then the solutions for x involve irrational numbers and
complex numbers. For example, the solutions for
, 1, 2. If, however, on this polynomial any sign is
incorrectly copied then the solutions for x involve irrational numbers and
complex numbers. For example, the solutions for ![]() are
are
![]() and
and ![]()
Could you have solved for these solutions?
Miscopying a single sign can change the character of a problem from a routine
one into a very formidable one.
Be careful throughout your mathematical work as you
go from one step to another. Working neatly will help a great deal to eliminate
mistakes arising from copying mathematical expressions incorrectly.
We have illustrated what can go wrong in a problem
with just a change in one sign. Think how bad it could get if a coefficient or
some other aspect of a mathematical expression is not rewritten correctly.
Mistake 9: Inverse operations: Which
direction do you really want to go?
The word “inverse” in mathematics generally means
“opposite.” If we are discussing the operation of addition, then the additive
inverse of a given number is a number when added to the given number gives 0.
If we are discussing multiplication, then the multiplicative inverse of a given
number is a number when multiplied by the given number gives 1.
Examples are:
![]() and
and ![]()
-5 is the additive inverse of 5 and ![]() is the multiplicative
inverse of 5.
is the multiplicative
inverse of 5.
The word “inverse” also applies to functions. Nice
illustrating examples are the function keys on your calculator. Do you have a
button labeled “![]() ?” Enter a number into your calculator, any number, say 5.
Push the
?” Enter a number into your calculator, any number, say 5.
Push the ![]() button. Push it again
and again and again. Notice that the display reads 5, then
button. Push it again
and again and again. Notice that the display reads 5, then ![]() , then 5, then
, then 5, then ![]() , . . . . You learned about functions and their inverses in
College Algebra and you will learn more in other mathematics courses that you
take. But one source of difficulty for some students is keeping straight which
direction you are going when working with functions and their inverses. As an
example, consider the log function. Do you have log as a function on your
calculator? If so you will notice that it is located on a button that has two
functions. Not only does the button have the log but it also has the inverse
function of the log. Experiment with this calculator by playing a game similar
to the one we played with the
, . . . . You learned about functions and their inverses in
College Algebra and you will learn more in other mathematics courses that you
take. But one source of difficulty for some students is keeping straight which
direction you are going when working with functions and their inverses. As an
example, consider the log function. Do you have log as a function on your
calculator? If so you will notice that it is located on a button that has two
functions. Not only does the button have the log but it also has the inverse
function of the log. Experiment with this calculator by playing a game similar
to the one we played with the ![]() button. Take a number,
any positive number. Enter it and push the log button. Next push the second function assigned to that key and see what happens. You get
back the number you started with. You have just seen another demonstration of a
function and its inverse. Because these functions are so closely related it is
easy to get them confused. Be alert to this potential difficulty as you study
inverse functions in Technical Calculus, especially when working with
trigonometric functions.
button. Take a number,
any positive number. Enter it and push the log button. Next push the second function assigned to that key and see what happens. You get
back the number you started with. You have just seen another demonstration of a
function and its inverse. Because these functions are so closely related it is
easy to get them confused. Be alert to this potential difficulty as you study
inverse functions in Technical Calculus, especially when working with
trigonometric functions.