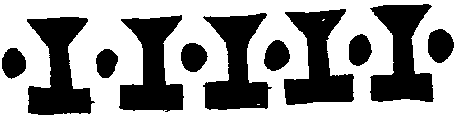
Charity Murdock
How We Classify Border Patterns
The classification system we use in class assigns to each border pattern a two letter/number code to label its type. There are the seven possible labels or codes based on their symmetry properties:
| Seven Border Types | |||
| 1m | 1g | 12 | 11 |
| mm | mg | m1 | |
This table summarizes the two letter/number code scheme.
| First Code Letter | Second Code Letter |
| m = vertical symmetry | m = horizontal symmetry |
| 1 = no vertical symmetry | g = glide reflectional symmetry |
| 2 = half-turn symmetry | |
| 1 = no additional symmetry |
A description (and examples) are given below for each of these symmetry concepts. The descriptions show how different groups of students expressed their understanding of these symmetries. Illustrative examples were provided by different student groups. This class is made up primarily of prospective elementary teachers. We try to express these concepts as a concrete, hands-on process.
First Code Letter
(Vertical Symmetry)
m_ -- Vertical or Crossline Symmetry
"This means that the pattern can be divided at some section and have identical patterns on each side of the dividing line. If the pattern was folded on the dividing line, the two sides would match up perfectly."
-- Renee, Selina, Heather, Travis and Amy
Example with Vertical Symmetry
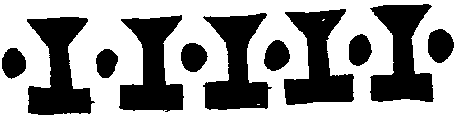
Charity Murdock
"Lay a mira vertically across the pattern. The reflection of the pattern fits exactly on the actual pattern."
-- Courtney, Charity and Jamie
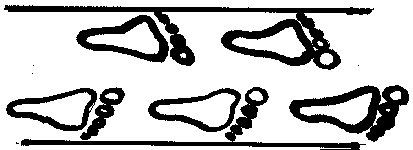
1_ -- No Vertical Symmetry
"If the figure doesn't reflect itself (when a mira is placed across the pattern), then it is classified with '1'."
- Eric, Terry, Becca
Example with No Vertical Symmetry

Travis James
Second Code Letter
(Horizontal Symmetry)
_m -- Horizontal or Midline Symmetry
"Draw a horizontal line through the middle of the pattern and if it reflects through this line, then the pattern will be classified with m."
-- Eric, Terry, Becca
"To decide if a border pattern has horizontal symmetry, place a mira lengthwise across the middle of the pattern. The pattern has horizontal symmetry if the image of side one reflects exactly onto side 2."
-- Shannon, Jackie, Cambor, David
Example with Midline Symmetry
Jamie Stearman
"If you can fold it onto itself along a horizontal line throught the middle, then it is an 'm.'"
-- Rhonda, Susana, Steven, Joie
_g -- Glide Reflectional Symmetry
"To decide this, with a clear sheet of paper, trace the design. Next, flip the sheet over and line it up with the pattern. Glide it to the right to see if the patterns line up."
-- Shannon, Jackie, Cambor, David
Example with Glide Reflectional Symmetry
David Wall
"To find glide reflectional symmetry, trace the pattern. Flip the paper top to bottom and place it over the original pattern. At this point, slide the paper to see if the patterns line up at any point. If they do, then it is a "g"."
-- Rhonda, Susana, Steven, Joie
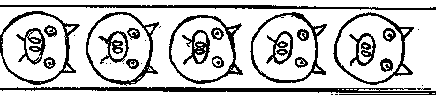
_2 -- Half-turn Symmetry
"Trace the pattern and turn the trace clockwise or counter clockwise so the top goes to the bottom and vice versa. If the pattern matches, then the pattern has type 2 symmetry."
-- Tiffany M., Amy P., Dianne, Susan
Example with Half-Turn Symmetry

Jamie Stearman
"To find half-turn symmetry you can trace over the border pattern and then give the traced pattern a half-turn. If the pattern lines up then it will be classified with a 2."
-- Eric, Terry, Becca
_1 -- No Additional Symmetry
"We use the mira and a piece of paper to see if the border has horizontal, glide reflection or half-turn symmetry. After testing with all these methods, we discover that the order has none of these and is a "1"."
-- Courtney, Charity, Jamie
Example with Half-Turn Symmetry

Tiffany Sims
Important Final Concepts
"Also note that if you get a type of symmetry for the seccond letter, like "m" it is possible to have another type of symmetry, like "g". But we only put one type down, in the order that the tests are presented here, i.e., if you get type "m" you don't have to check any other types."
-- Tiffany M., Amy P., Diane, Susan
Classified _m (but also has type _g and _2)

Tiffany Mayer